Advanced consulting theory 1: parsimony (why you were hired)

"Consulting" work once connoted expert guidance. The past 25 years of tech work muddied that definition to include "anyone who bangs on a keyboard"—engineers, designers, testers, data scientists, vibe coders, and Agile Certified PMP Scrum Masters alike!

If predictions about AI hold true, then digital's undergoing its own "CNC machining moment". The labor requirement of mass tech production will shrink dramatically…but true expertise in this reshaped context will become considerably more precious.

If you're in a consulting role, you'll need to operate at an elevated level. In this first of many parts, we explain advanced consulting theory concepts you should understand and apply.

Any formula too accurate loses its predictive (guiding) utility. That may sound counterintuitive in our era of more-is-better, big-data correlation-driven logic but it's a demonstrable statistical and scientific fact. That same deterioration of guiding utility also applies to strategies, plans, advice, and their execution over a given business cycle. Anything overdone will be overly fragile when faced with the slightest change:

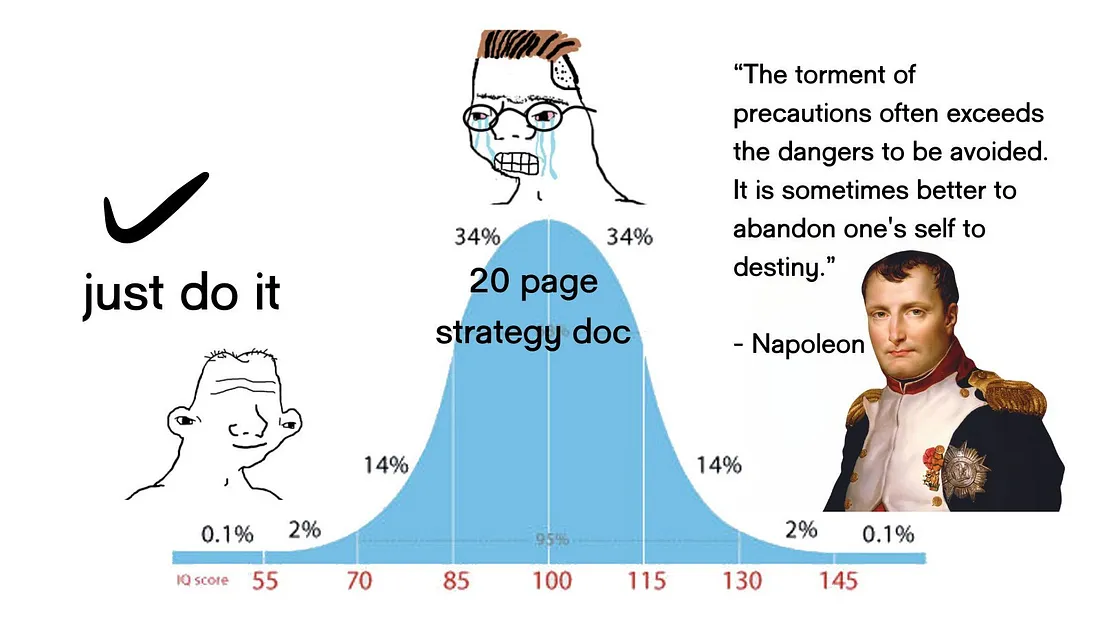
When business leaders implore their employees to act, they still expect consideration to occur first. "Action bias" does not mean renouncing critical thought—it means knowing when you've got enough to go. Parsimony focuses thought and transforms action into meaningful action.

Clear away the years and the haze and reflect on your high school science classes. You may recall the cycle that is the scientific method:

1. Make an observation or ask a question
2. Research subject area to focus inquiry
3. Formulate hypothesis
4. Test hypothesis with experiments
5. Analyze data
6. Report conclusions
7. Repeat and refine

While it's easy to confound science with raw, machine-like objectivity, the messy realities of nature ensure science isn't that simple. Several metaconditions exist inside the scientific method, affecting a scientist's targets and outcomes, the most prominent of which live in the PEL model:

• Presuppositions—beliefs and conditions required to reach a conclusion
• Evidence—measured information that arbitrates between theories
• Logic—correct reasoning and proof rated by deductive validity (yes/no) and inductive strength (probability)

Most of the scientific theory and example presented in this article comes from chapter 8 of Scientific Method in Practice by Hugh Gauch—the only signed academic textbook I own! You'll level up if you read this book. As Gauch says, "every scientific conclusion, if fully disclosed..." invites examination of these three premises.

Between Gauch's P, E, and L, evidence always feels like the obvious part, the glossed-over middle child, even to trained scientists. "Oh, there's the data." Unlike presuppositions and logic, evidence creation and handling tends to be extremely domain-specific (but...objectivity!) with good reason: measuring say, air currents, then understanding what that measurement means is a hyperspecific thing.

The one great exception to this, a general principle that applies to evidence across disciplines: parsimony. While most people think "prefer simpler models" encompasses everything they need to know, consultants like you should understand that the training curricula and work experience of high-falutin' MBA consultants and Ph.D scientists neglects genuine training on parsimony. If you want to differentiate your expertise, start here.

Most consider Ockham's razor the embodiment of parsimony in practice:

"Of two competing theories, the simpler explanation of an entity is to be preferred."

Parsimony in practice is a problem-solving heuristic that recommends searching for explanations constructed with the smallest possible set of elements because tighter theories are more testable (or actionable), more explicable, and frequently more accurate. Parsimony balances fit with simplicity.

A parsimonious scientific theory or consulting recommendation will be:

• Predictive (guiding), offering a likely outcome
• Explanatory, ideally self-explanatory and connected to a core "why"
• Testable or actionable
• Insight-generating
• Repeatable
• Coherent with other context (not a wacky non-sequitur)

In both science and business consulting, there's a looming temptation to make one's theory fit the data, resulting in sometimes absurd conclusions fervently defended with ad hoc hypotheses until they collapse under their complexity or irreplicability. Parsimony's naturalistic in the sense that evolutionary nature dispenses with unnecessary complications, whether physiological features or whole species themselves.

So, be like nature. Among theories fitting data equally well, scientists should therefore choose the simplest. Among options fitting a client's needs equally well, consultants should advocate the simplest. Especially if they want to see them executed.

What always gets missed is why investigators, thinkers, and consultants should be parsimonious. The ultimate reason: simple survives.

Scientists' theories face the prospect of outside testing, replication, critique, unplanned conditions piled on by other professional scientists. At the most basic level, simpler theories can be tested and replicated more easily. Similarly, consultants' strategic recommendations must weather:

• Executives' whims
• Rampant miscommunication
• Disparagement from competing internal groups
• Stakeholder firings (or worse, hirings)
• Market fluctuations
• Intractable dependencies
• Random and ridiculous externalities

Complex recommendations are fragile at best, laughable at worst. On top of that, businesses can implement simpler recommendations more readily, leading to a higher likelihood of success or failure being proven one way or another instead of yet more consultant-led churn.

Parsimony should influence thought—it's not irrefutable and not meant to be. Think of parsimony as a force of logic pressuring you to fight your very human urge to be right, overfitting your theory to your data (or selecting your data for your theory), or otherwise overcomplicating matters and confusing your stakeholders. Moreover, as it turns out (described later below), a stronger fit, or more "correctness", makes models and recommendations less useful.

Be advised, there's a darker path to simplicity in science and consulting: beauty. Quoting David Orrell:

"People seek out partners with symmetric facial features because they are considered attractive. Physicists seek out symmetries in nature because these allow them to produce simplified mathematical representations (and because they are considered attractive).

Another famous example of a beautiful theory is Einstein's E=mc2, which unifies the concept of energy (E), mass (m), and the speed of light (c). The equation grew out of Einstein's theory of relativity, which his colleague Max Born called 'a great work of art, to be enjoyed and admired from a distance.'"

Beautiful theories and strategies look and sound right enough to mask any inherent hollowness or falseness. They're utterly seamless, like an actor playing a genius.

Scientists and consultants alike face the temptation of beauty in thought and analysis, whether convenient solutions, "quick wins", slogans, targeted terminations, or up-and-to-the-right charts. Perceptible elegance possesses an allure so spellbinding that only disciplined minds can separate ideas cast by Hollywood from those forged by evidence. Enamored stakeholders may prove impossible to detach from a seductive idea. There's no worse pain than abandoning a beloved position for an ugly, practical truth.

Any engineer can tell you simplicity isn't simple. It's even less simple for scientists.

Creating theory to explain the world

When scientists create a formula to explain data, their process isn't as simple as pure maths. A scientist accounts for five core ideas that do apply to consulting:

1. Signal and noise. Data are imperfect and never wholly self-explanatory. In scientific analysis, signal refers to data consisting of response to an experiment's treatment factors. Noise represents uncontrolled variances, like the individual differences between lab rats or the nutrients in their food. Consultants often dedicate significant effort to helping their customers separate the two.
2. Population vs. sample data. If a scientist is investigating daffodils, the population is the term for all daffodils in the universe. The sample is the segment of daffodils that scientist experimented with and collected data about plus the specifics about that scientist's treatments—data being collected only during daytime or during rain, for example. Data's always limited, and all data were derived from samples and all samples were chosen (what/where/when/how to measure). Consequently, there is no "all the data", even with massive compute and sensing capabilities.
3. Prediction vs. postdiction. Prediction = accuracy to population, postdiction = accuracy vs. sample. Statistically, predictive and postdictive models reach peak accuracy at different places: post at max complexity, pre much sooner. As a consultant, you don't have infinite time and as a business serving a fickle market, neither does your client. Postdiction's ultimately more accurate, of course (against its sample data), but it's more work, more fragile, and instantly invalidated when context changes. Optimization for population vs sample sets will look different.
4. Curve fitting. In science, curve fitting is the process of finding a mathematical function to describe a relationship between variables that can help explain (or define) the experiment's treatment effect. The closest analogy in consulting is either problem diagnosis or, more likely, solution design. If you've found yourself tweaking, adjusting, parameterizing, qualifying, and equivocating about your solution, you're curve fitting. Trouble is, the right fit may not be the right answer!
5. The nature of change. Centuries of scientific analysis have shown that, observationally, change in physical, chemical, and biological systems tends to occur along simple and smooth lines, not hard breaks. Every veteran consultant knows that while a stakeholder may crave drastic, breaking change, laws of nature still apply. Few organizations can survive sharp pivots, and stark change is rarely desirable if the status quo is working enough for them to afford you…

Give me the answer

Taking all of that smart science talk into account, the trimmest method consultants can follow to create parsimonious strategic and tactical recommendations is:

1. Locate the signal (patterns, behaviors, aversions preventing success)
2. Capture the relevant signal until you detect noise, then stop (mechanisms and contexts driving the above)
3. Model the essence of the problem ("phenomena a, b, and c cause org to ____")
4. Communicate the essence of your solution ("change x to get/stop y and z")
5. Operate the executive sequence until reaching your declared v1 state (run plan results + insight tack course)

Sounds simple in practice, but you'll need further theoretical understanding to master the method. Continue on!

Yes, Ockham's hill is named for the Ockham's razor guy, William of Ockham, but was not identified by him. Ockham's hill illustrates the concept of statistic efficiency, the measurement of the quality of an estimator in a given model. Statistical efficiency affects recommendations, strategies, and formulas alike.

Where precision and accuracy diverge

A simple model can outperform its own data. How so? Because sample data contains noise.

As touched on above, a model's (or curve's) fit to a dataset reflects its both its efficiency and predictive power. An underfit model is one whose parameters don't explain enough to be predictive against a population. An overfit model is on whose parameters tightly fit sample data (including noise) and loses predictive power against population data.

Statisticians have done a lot of work in the past 50+ years to unpack how sample-derived scientific models work vis-a-vis both sample and population data. It turns out that when build a formula to fit a dataset and create predictive power, early parameters (not always first parameters) capture most of the signal, doing most of the heavy lifting for the model's explanatory capability. Simplistically, if your formula is:

Y = ax² + bx⁵ + cx² + d

It's extremely likely that one of those parameters explains the bulk of the signal, while the remaining parameters filter (or capture) the data's noise, generating an efficiency curve like so:

Therefore, an efficient, predictive, low p-value model:

1. Collects mostly signal early in analysis
2. Reaches a maximum efficiency point or plateau (Ockham's hill/Goldilocks zone)
3. Detects or handles increasing noise as it's overfit to the sample

Clean data supports more parameters and more computation, therefore pushing Ockham's hill further right on the x-axis or flattening it altogether. Reality's messy, though, even in science, and that means noise. If there were no noise, there'd be no Ockham's hill. Complexity would be perfect and tolerable, and complicated, feature-laden cars would break down at the same rate as simple cars.

Worse, statistical modeling of complex polynomials with four or more parameters shows that an infinitude of equally plausible alternatives to a given four-parameter will exist. If you've presented a complicated plan, then comparisons between your paid consulting recommendation, others' free recommendations, and the incumbent status quo become impossible to anyone without oodles of time, attention to detail, and a penchant for hair-splitting (so, zero executives).

Beware the "collecting data" person

Leaning into statistical efficiency, scientists routinely find it cheaper and more effective to work on and/or rethink their explanatory models than it is to collect data. Aggressive early theory/modeling outperforms considered action and intuitive data collection which itself outperforms rash action.

If you've sat across from the "collecting data" person—the one who's ever-heistant to make a judgment until the last possible moment while their passivity makes everyone else doubt their own theory and action—don't fall for their shenanigans. He, she, or they may indeed be observing carefully, but they're not thinking around the next corner enough to separate signal from noise. Now you know why this individual always sounds smart but isn't genuinely effective!

The 80/20 rule is real!?

Consultants, did your client equip you with clean data? Do you have complete data about them and their strategic conundrum? No? Then There Will Be Noise, and that's OK.

The essence of what you need to deliver to your client and what your clients needs from you lives atop Ockham's hill. The question is whether or not someone on your team is listening for the signal you need to do right by the customer. In a new and confusing consulting engagement, time-wasting bullshit like weeks of interviews and design sessions can rack up billable hours, but tends to underperceive relative information acquisition relative to what's necessary to help your client. Amateur consultants:

• Undershoot signal with off-target exercises that don't produce the information needed to solidly proceed.
• Overshoot signal, learning what they need to learn early enough, then re-learned it many times over.

Whether you're factfinding, recommending a go-to-market strategy, or creating an enterprise architecture, working to Ockham's hill (or, in the parlance, knowing when to quit) makes your work:

• Faster
• More comprehensible
• More transmissible
• More meaningful
• More effective
• Less burdensome

Getting a sense for Ockham's hill gives your work high meaning and high comprehensibility. So, as you engage a challenge, ask:

• Am I detecting signal about my client's challenge?
• Do I have enough signal to make likely sense of my client's situation?
• Did I capture enough signal to make a recommendation with a high-enough probability of utility?

If so, you're doing it right. At last, scientific justification for the (consultant-built) 80/20 rule! Do less, focus more, achieve better!

Parsimony vs. tailored solutions

Parsimonious recommendations apply primarily to strategies. Parsimony and the Pareto Principle don't let you off the hook when it comes to formulating a tactical implementation. All the overthinking you've done about your highly-tailored technology solution is still valuable if the base strategy it rests upon remains robust and survivable. Your bespoke solution ("a custom Javascript-based ERP…") is almost certainly hyper-tactical relative to the core strategy ("move ERP to cloud because X, Y, Z").

That said, you'll never have the information you need for a perfect recommendation or solution. If you did, so would your customer. Wait, why are you here, again?

Direct data describes the singular measurement of a lone sample. Indirect data refers to accounts for all other data points as well. Consider this matrix taken from Gaugh's Table 8.1, borrowed from Lide (1995:5–87):

Equivalent conductivities (Ω^-1 cm² equiv^-1) of aqueous solutions of hydrochloric acid at various concentrations and temperatures

Concentration (mol l-1)	25 °C	30 °C	35 °C
4.5	183.1	196.6	209.5
5	167.4	?	191.9
5.5	152.9	165.0	175.6

How would you get the missing data point? You could:

1. Take a direct measurement
2. Build and apply a model
3. Calculate the average of all the other data points

Method 1 requires measurement, Method 2 requires scientific analysis and postulation, and Method 3 just arithmetic. Ironically, depending on your sampling error rate, direct measurement may be the least reliable.

Each approach can yield a close-enough result (~180.2). Method 3 succeeds by using related, indirect data—data containing information about the same relationship we're investigating, but not for the specific sample or situation we're looking at. Simple models often outperform their data because they leverage indirect information. In so doing, they infer a relationship, a pattern between factors that matter (signal) at the exclusion of things that don't (noise). In business, we call this phenomenon "experience".

In consulting, clients provide plenty of direct data specific to their moment, market, and challenge. You'll use their direct data to design and execute your solution.

However you, dear consultant, deliver parsimony to your clients by supplying the related, indirect data their experts cannot otherwise obtain. That's why you're there. Consultants accelerate simplification and resolution by applying their indirect experience to their customer's direct challenge. Don't forget that.

Part 2 focuses on the reciprocal half of parsimony: your client's real ability to absorb your consulting.

---

Next Mile consulting helps businesses navigate troublesome technology transitions. If you need guidance from experts who truly care about the effect of our work, contact us today.